The prediction of flow-induced noise emissions can be achieved by coupling a CFD and a CAA solver in the so-called direct-hybrid method. The CFD solver yields the flow field, while the CAA solver computes the acoustic field by solving the acoustic perturbation equations (nmAPE) using acoustic source information from the CFD solver. In m-AIA the direct-hybrid method utilizes the DG solver for the CAA, while the flow field can be solved using the FV or LB solver.
Parallel coupling algorithm
Source: Schlottke-Lakemper2019
Note: the following refers to the FV-DG coupling.
To avoid execessive idle times due to different workload compositions of both solvers on each rank, it is necessary to interleave the solvers during the execution of a single time step. The systems are alternately advanced by one substep. The figure below shows an example of the interleaved execution pattern for one complete time step and two solvers with \(n_A = n_B = 3\) substeps. Due to the interleaved execution, no overhead is created by having different proportions of cells for each solver on any subdomain assuming one intra-solver communication between two substeps. On subdomains, where both solvers are present, it is even possible to overlap the communication of one system with the computation of the other system.
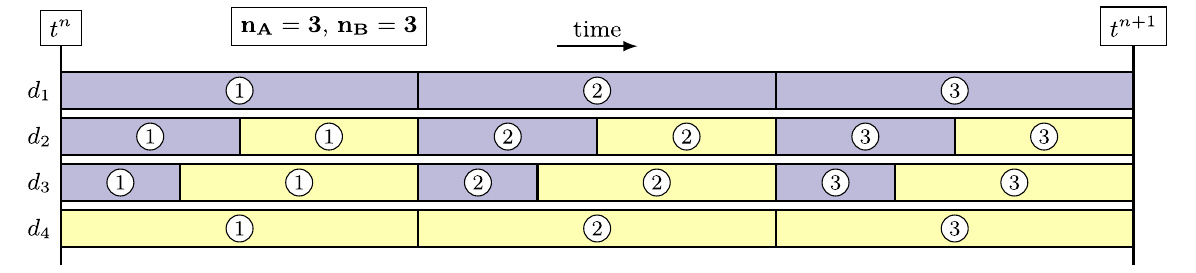
See also: Dynamic load balancing (DLB)
Spatial interpolation
Source: Schlottke-Lakemper2019
Note: the following refers to the FV-DG coupling but applies also for, e.g., LB-DG coupling.
In hybrid aeroacoustics simulations, at each time step, source term data has to be transferred from the CFD simulation to the CAA simulation. In addition, the mean flow solution needs to be available on the CAA mesh. Since the cells of the shared hierarchical grid that are used by each solver may differ, a spatial interpolation scheme has to be employed to map the data from one solution representation to the other.
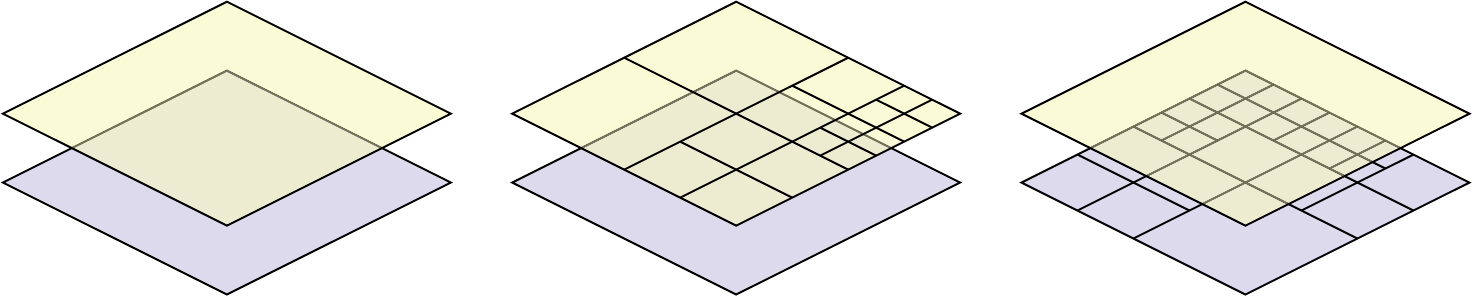
In general, there are three types of spatial mappings. If the CFD cell and the CAA cell have the same size, a single source term for each variable is calculated on the FV-CFD cell and then used on all Gauss nodes of the corresponding DG-CAA element. The same approach is also used for one-to-multiple mappings, where one CFD cell is mapped to multiple CAA cells. In the third case, there is a multiple-to-one relationship between several FV-CFD cells and a single DG-CAA cell. This situation is typical for high-order DG-CAA simulations, where the large number of Gauss nodes per DG element allows to reduce the refinement level of the CAA grid in the source region. For this type of mapping, the source terms have to be transferred from the piecewise constant representation of the finite-volume grid to the high-order polynomial representation of the discontinuous Galerkin grid using a suitable interpolation method.
Besides computational efficiency considerations, it is important that the selected scheme does not lead to additional MPI communication. Furthermore, it is desirable to have a conservative mapping routine to correctly reproduce the acoustic pressure that is generated by the source terms. One possible choice for FV-to-DG interpolation is the local Galerkin projection method proposed by Farrell and Maddison, which is used to derive a projection operator in the following. Fundamentally, the interpolation of a field \(q\) from a donor mesh \(\mathcal{T}^D\) to a target mesh \(\mathcal{T}^T\) is sought. No assumptions are made as to the field or the meshes. For the CFD-CAA coupling, the field \(q\) represents the acoustic source terms and the donor and target meshes correspond to the CFD and the CAA grids.
The representation of the field \(q\) on a cell of the donor mesh \(K^D \in \mathcal{T}^D\) is given by \begin{equation} q^D = \sum\limits_{i=1}^{\mathcal{N}^D} \hat{q}^D_i \phi^D_i,\label{eqn:q_d} \end{equation} where \(\{\phi^D_i\}_{i=1}^{\mathcal{N}^D}\) is a set of \(\mathcal{N}^D\) basis functions with \(\phi^D_i = \{\phi^D_i(\mv{x}) | \mv{x} \in K^D\}\) and \(\hat{q}^D_i\) are the coefficients. Likewise, the interpolant \(q^T\) of the field \(q\) on a cell of the target mesh \(K^T \in \mathcal{T}^T\) is defined by \begin{equation} q^T = \sum\limits_{i=1}^{\mathcal{N}^T} \hat{q}^T_i \phi^T_i,\label{eqn:q_t} \end{equation} where \(\hat{q}^T_i\) are the coefficients corresponding to the \(\mathcal{N}^T\) basis functions \(\phi^T_i= \{\phi^T_i(\mv{x}) | \mv{x} \in K^T\}\). First, the special case of a one-to-one mapping between the donor and target cells is considered, i.e., \(K^D = K^T\), which will later be generalized to interpolating multiple donor cells to a single target cell. The interpolant \(q^T\) shall be optimum in the \(L^2\) norm [That] is, \begin{equation} |q^D - q^T|_2 = \min_{\tilde{q} \in \mathcal{V}^T} | q^D - \tilde{q}|_2,\label{eqn:ansatz_galerkin_projection} \end{equation} where \(\mathcal{V}^T = \text{span}\{\phi^T_i\}\) for \(i = 1,\ldots,\mathcal{N}^T\) is the function space spanned by the basis \(\{\phi^T_i\}_{i=1}^{\mathcal{N}^T}\) of the target mesh. The left-hand side of \(\eqref{eqn:ansatz_galerkin_projection}\) is minimized if its derivative with respect to the coefficients \(\hat{q}^T_i\) is zero, i.e., if \begin{equation} \frac{\partial}{\partial \hat{q}^T_j} |q^D - q^T|_2 = 0, \qquad j = 1,\ldots,\mathcal{N}^T.\label{eqn:minimization_equation} \end{equation} After expanding the definition of the \(L^2\) norm, this yields the defining equation for the interpolation operator \begin{equation} \int\limits_{K^T} q^D \phi^T_j d \mv{x} = \int\limits_{K^T} q^T \phi^T_j d \mv{x}, \qquad j = 1,\ldots,\mathcal{N}^T.\label{eqn:projection_definition} \end{equation} Since the sought interpolant \(q^T\) is defined on the target cell, the domain of integration is \(K^T\). Since the interpolant obtained through this approach is optimum in the \(L^2\) norm, the method is referred to as Galerkin projection (FarrellMaddison11). The conservation property of the scheme follows directly from \(\eqref{eqn:projection_definition}\) for \(\phi_j^T = 1\).
If multiple donor cells are mapped to a single target cell, the integrand on the left-hand side of \(\eqref{eqn:projection_definition}\) may contain discontinuities, since the field \(q^D\) is generally discontinuous across cell boundaries. In this case, the integral over the target cell \(K^T\) is split into \(S\) integrals over each contributing donor cell \(K^{D,m} \in K^T\) with \(m = 1,\ldots,S\), where \begin{equation} K^T = \bigcup\limits_{m=1}^{S} K^{D,m}. \end{equation} For multiple donor cells, \(\eqref{eqn:projection_definition}\) can then be rewritten to \begin{equation} \sum\limits_{m=1}^{S}\left(\,\,\int\limits_{K^{D,m}} q^{D,m} \phi^T_j d \mv{x}\right) = \int\limits_{K^T} q^T \phi^T_j d \mv{x}, \qquad j = 1,\ldots,\mathcal{N}^T,\label{eqn:projection_definition_multi} \end{equation} where \(q^{D,m}\) is the representation of the field \(q\) on the donor cell \(K^{D,m}\).
When interpolating the source terms from a finite-volume representation to a discontinuous Galerkin representation, the general projection operator can be simplified, since only piecewise constant to polynomial interpolation must be considered. For the finite-volume method, \(\mathcal{N}^D = 1\) with the constant basis function \(\phi^D_1 = 1\) and thus \(q^D = \hat{q}^D_1 =: \hat{q}^D\). In the DGSEM, the interpolant \(\eqref{eqn:q_t}\) is \begin{equation} q^T = \sum\limits_{i,j,k=0}^{N} \hat{q}^T_{ijk} \psi_{ijk}(\mv{\xi}),\label{eqn:q_t_dgsem_} \end{equation} where \(N\) is the polynomial degree and with \(\mathcal{N}^T = (N+1)^3\) Lagrange basis functions \(\psi_{ijk}\) for \(i,j,k = 0, \ldots, N\) (Derivation for cube-shaped elements). Inserting these definitions for \(q^D\) and \(q^T\) in \(\eqref{eqn:projection_definition_multi}\) and replacing the integrals by Gauss quadrature, the interpolant \(q^T\) is obtained as \begin{equation} \hat{q}^T_{ijk} = \sum\limits_{m=1}^S \hat{q}^{D,m} \widehat{W}_{ijk}^{D,m},\qquad i,j,k=0,\ldots,N,\label{eqn:projection_dgsem_} \end{equation} where \(\widehat{W}_{ijk}^{D,m}\) represents the relative weight of the contribution of donor cell \(K^{D,m}\) to the \(ijk\)-th Gauss node. Details on how to determine the weights \(\widehat{W}_{ijk}^{D,m}\) and an analysis of efficient implementation strategies can be found in Schlottke-Lakemper2019.
References:
- M. Schlottke-Lakemper, A. Niemoeller, M. Meinke, W. Schroeder, Efficient parallelization for volume-coupled multiphysics simulations on hierarchical Cartesian grids, Computer Methods in Applied Mechanics and Engineering, Volume 352, pp 461-487, 2019, 10.1016/j.cma.2019.04.032.
- P. Farrell, J. Maddison, Conservative interpolation between volume meshes by local Galerkin projection, Comput. Methods Appl. Mech. Eng. 200 (1–4) (2011) 89–100, 10.1016/j.cma.2010.07.015.