General Solution Step
Cut-cell generation
For moving boundaries, Cartesian cells are reshaped according to the local penetrating boundary of a moving body. That is, the Cartesian cell is cut according to the position of the boundary surface embedded inside the cell borders and its volume is adjusted accordingly. Multiple cuts through a single Cartesian cell are possible which allows for the resolution of, e.g., two colliding bodies, on a sub cell-size level.
The cut-cell generation is a stepwise process which relies on accurate levelset information of the embedded bodies. Hereafter, the term levelset information will refer to a signed distance function \( \phi \) in which positive values mark the outside- and negative values mark the inside of a body. The exact boundary position is then located at a levelset value \( \phi = 0 \).
The overall process can be broken down as follows. First, the body information, as represented by their cell-centered levelset values, are transferred into the FVMB solver (FVMB). All boundary cells are then marked according to the cell-centered levelset information. The levelset data is subsequently transitioned from cell-centered to nodal-centered, i.e., each Cartesian cell has one, or in case of a multi levelset approach, multiple, levelset values assigned to each of its eight nodes in three-dimensional space (or four nodes in two-dimensional space). The information is transformed by using a distance-based interpolation/averaging of all cornering cell-centered levelset values. Multiple levelsets are supported. Due to the utilized parallelization methods, the nodal values are exchanged afterwards on halo cells with neighboring domains. Based on the nodal levelset information, distinctions of cells being active, and thus have part fluid, and inactive can be made. That is, cells, which are fully immersed in a body represented by a moving boundary, are deactivated and skipped from the temporal integration.
Note that the aforementioned process differs for an analytical levelset (ANAL-LS). For ANAL-LS, the nodal values are not computed from the cell-centered levelset information, but rather are computed as a signed distance value from the n-dimensional location each nodal point to the nearest surface.
Subsequently, the nodal values of all active cells are checked for differing mathematical signs in relation to its neighboring nodal value, see
. Here, a mismatch in signs characterizes a pass through \( \phi = 0 \) and thus, a boundary surface.
[fig of 3d cube with nodal example ?]
In case of differing signs, the location of the cut point of the boundary surfaces is determined by interpolating between both nodal values. Once all boundary surface cut points are determined ....
Ghost cell boundaries
In the following description of the ghost cell boundaries the problem is reduced to single cut surfaces. However, the procedure is also suitable for multi cut cells.
In figure (Cut cells with corresponding ghost cells) the general procedure can be seen. The boundary condition is imposed by a ghost cell which is located outside the actual computational domain mirrored to the cut surface. The cut cell and the ghost cell share the same volume. However, as can be seen in comparison of figures A and B, the normal distance between the cut surface and the ghost cell center is different. The distance is determined by formula \(\eqref{eq:distGhost}\).
\begin{equation} l = \max \left \{ d, \frac{cellLength}{2} \right \} \label{eq:distGhost} \end{equation}
Where \(l\) describes the normal distance between the ghost cell and the cut surface, \(d\) corresponds to the normal distance between the resulting volumetric center of the cut cell and the cut surface, and \(cellLength\) is the edge length of an uncut grid cell. This differentiation is chosen to prevent the ghost cell distance from shrinking reciprocally to the cut cell. Thus, the negative influence of small cells on the numerical stability can be significantly reduced. The volumetric center of the ghost cell and the volumetric center of the cut cell are located on an axis normal to the cut surface.
Image point
To prevent asymmetric spacing, an image point can be inserted which has the same distance \(l\) as the ghost cell to the surface. Due to this condition it can be either inside the cut cell or even in the area of the inner neighbours. The variable value at the image point location is determined by a least squares method which includes the surface value and a 2 cell wide (also diagonal) stencil.
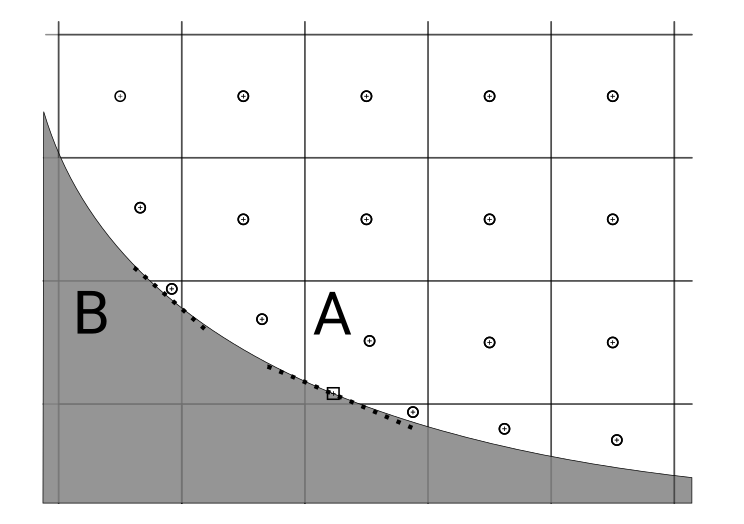
The support points
for neighbouring cells and
for the surface point used in the procedure for cell A are highlighted in the graph (Grid section with boundary surface). Especially for the calculation of the heat transfer coefficient it is crucial that the surface is located midway between the ghost and the cut cell center.
The image point can be used to impose the boundary condition.
Small cell correction
The above described approach carries the the risk of generating cells with arbitrarily small volumes, which, if left untreated, could indefinitely reduce the stability of our numerical method. A small cell correction can solve this problem (SCC).
