Source: Niemoeller2020 (consult paper for references)
The ultimate goal of dynamic load balancing is to maximize the overall performance of a parallel computation by redistributing the workload among processes such that all available computing power is used to full capacity (Hendrickson2000a). Load balancing in highly parallel applications is key for an efficient resource usage (Ashby2010), since even minor imbalances can have a severe impact on the performance and scalability of the computation. Numerical simulations typically involve frequent communication between MPI subdomains such that an aggravation of imbalances will occur in every iteration or stage of a time step due to synchronization (Boehme2014). Furthermore, the performance penalty is sensitive to the specific imbalance pattern, which is highly problem dependent. A single overloaded process will significantly degrade performance. The reason for this is that all other processes wait and sit idle until the communication among neighboring domains can proceed. On the other hand, a few underloaded processes will only have a minor impact on the overall performance. Finally, imbalances can be classified as dynamic or static (Boehme2014). Dynamic imbalances arise if the workload distribution varies as a function of time, which occurs, for example, when solution adaptive meshes are used. Constant workload distributions will lead to static imbalances.
Load imbalances and the resulting performance impact can be quantified by different metrics. Here, the imbalance percentage (DeRose2007) defined by
\begin{equation} I_{\%} = \frac{(t_{max} - t_{avg})\cdot N}{t_{max}\cdot(N-1)}, \label{eqn:imbalance_percentage} \end{equation}
which expresses the severity of an imbalance, is used. The quantities \(t_{max}\) and \(t_{avg}\) represent the maximum and average time to process a given section of code and \(N\) is the number of parallel processes. The imbalance percentage is defined by the ratio of the total amount of time wasted \((t_{max}-t_{avg}) \cdot N\) to the amount of parallel resources \(t_{max} \cdot (N-1)\). A value of \(I_\%=0\%\) corresponds to a perfectly balanced load distribution, while \(I_\%=100\%\) is associated with a code section executed only on a single process. Thus, the metric indicates the amount of wasted resources. This assumes that all but the slowest process sit idle at the end of the corresponding code section, which can be related to the completion of a single time step or stage of a time integration scheme in a numerical simulation. The potential run time savings are expressed by the imbalance time \(I_t = t_{max} - t_{avg}\) assuming that perfect load balance can be achieved (DeRose2007). Furthermore, the allocation-time impact is estimated by \(I_T = N \cdot I_t\), which is an upper bound on the total amount of wasted resources (Boehme2014).
In general, such a DLB algorithm needs to identify load imbalances, determine the amount of workload to be transferred, select corresponding objects to migrate, and finally, perform the relocation.
Dynamic load balancing of large-scale coupled multiphysics simulations is inherently complex and poses various challenges. For instance, multi-stage calculations and interleaved computations with inherent communication barriers may prevent load balancing (Hendrickson2000, Watts1998). The direct-hybrid method which couples an FV-CFD and DG-CAA solver is an example for such a coupled multiphysics simulation and even for static load distributions, a parallel computation might exhibit load imbalances.
Without load balancing, the parallel efficiency of the overall computation is determined by the initial domain decomposition, which is based on estimates regarding the different computational costs for CFD and CAA cells. These estimates can be determined by relating measured run times obtained from independent CFD and CAA simulations. However, this approach does not take into account the idle times of all parallel subdomains or, for example, boundary conditions that might be computationally more expensive. Consequently, the predicted load might deviate significantly from the actual load on each parallel subdomain during the coupled simulation (Jetley2008).
This performance impact is exacerbated when considering large-scale simulations with relatively small domain workloads or when using heterogeneous computing hardware (Dongarra2011). Then, a DLB method is required that automatically redistributes the computational workload to reduce imbalances during the simulation. In the direct-hybrid method, load balancing requires the redistribution of mesh cells used for the fully-coupled CFD/CAA solver, implicitly ensuring locality of the coupling acoustic sources. Furthermore, if the flow and the acoustics domain are of different size, a change of the grid partitioning can change the list of used parallel processes for each solver.
The present DLB algorithm is based on measurements of the computing time on each parallel process and the current distribution of cells of all solvers in all subdomains, new computational weights are computed. These weights are then used to determine a new domain decomposition.
Estimation of computational weights
Key to partitioning and load balancing of coupled multiphysics simulations is the estimation of computational costs for different objects present in the simulation (Menon2012). By objects the constituent parts of the numerical setup, i.e., cells of the grid, are meant. The standard approach for single-solver frameworks aims at distributing objects evenly among all parallel subdomains, assuming a homogeneous computing environment and likewise constant computational cost of each object. However, this poses difficulties if multiple types of objects with dissimilar computational costs exist. This problem can be reduced by using a-priori determined computational weights for each object type, which for the direct-hybrid method includes CFD and CAA cells. However, for complex applications this will often yield a suboptimal load balanced domain decomposition, due to inaccurate computational weights, which do not take into account the computational effort of all involved algorithmic elements or inhomogeneous computing hardware.
The implemented DLB algorithm estimates computational weights based on measurements of the computing time on each parallel subdomain. Furthermore, the current distribution of objects of the distinct solvers among all subdomains is incorporated. These types of objects, which can be regarded as different load types, give rise to varying load compositions. During the simulation, the collective compute time of all solvers and couplers is measured locally for each time step.
On each subdomain \(i\), the average compute time \(r_i\) is determined as the \(25\%\) truncated mean to filter out program-external influences such as system noise (Boehme2014,Petrini2003). With the global average compute time among all \(N\) parallel processes given by
\begin{align} \overline{r} = \frac{1}{N}\sum_{i=0}^{N-1} r_i, \end{align}
the local computational load \(l_i\) is determined as
\begin{align}\label{eq:load} l_i = \frac{r_i}{\overline{r}}. \end{align}
Subsequently, the computational weights \(\mv{c}\) for the different load types can be estimated by solving the least squares problem \(\mv{A}\mv{c} = \mv{l}\), with the right-hand side given by the load vector \(\mv{l} = \left(l_0, l_1, \dots, l_{N-1}\right)^\top\) and the left-hand side matrix \(\mv{A}\) representing the current workload distribution among all subdomains discussed in Fig (SFC example). This assumes that on average the load can be expressed as a linear combination of the individual workload contributions. The linear least-squares problem with unique minimum-norm solution can be written as
\begin{align}\label{eq:weights_leastsquares} ||\mv{Ac}-\mv{l}||_2 = \min_{\mv{v}} ||\mv{Av} - \mv{l}||_2 \quad\text{and}\quad ||\mv{v}||_2 \text{ is minimal.} \end{align}
The Eigen library is used to solve the least-squares problem given in Eq. \(\ref{eq:weights_leastsquares}\). An example for this procedure with two load types distributed among \(N = 4\) parallel subdomains is given in Eq. \(~\ref{eq:weights_example}\). Solving the overdetermined system of linear equations in the least-squares sense yields a computational weight ratio of \(2.61\) between the two load types. Thus, the average compute time for the second object type is estimated to be 2.6-times higher than that of the first one.
\begin{align} N \left\{ \begin{bmatrix} 10 & 7 \\ 13 & 4 \\ 12 & 2 \\ 5 & 8 \\ \end{bmatrix} \right. \begin{bmatrix} c_0 \\ c_1 \\ \end{bmatrix} = \begin{bmatrix} 1.2 \\ 0.9 \\ 0.8 \\ 1.1 \end{bmatrix} \Leftrightarrow \mv{A}\mv{c}=\mv{l} \quad \Rightarrow \quad \mv{c} = \begin{bmatrix} 0.0420 \\ 0.1097 \\ \end{bmatrix} ,\quad \frac{c_1}{c_0} = 2.61. \label{eq:weights_example} \end{align}
Partitioning approaches
Hilbert space filling curve partitioning
The partitioning of the computational grid takes place on the partition level, where a Hilbert space-filling curve is used to obtain a one-dimensional ordering of all partition cells. Each cell of the grid is assigned a computational workload depending on its use by either one or both solvers. By traversing the subtrees of the grid, the accumulated workload for each coarse partition cell is then determined. Thus, the parallelization is reduced to a so-called chains-on-chains partitioning (CCP) problem (Pinar2004).
That is, a chain of weighted computational tasks is contiguously mapped onto a chain of parallel processes. Consequently, a domain decomposition can be obtained by splitting the one-dimensional workload distribution into partitions of similar total workload. The approach is illustrated in the figure below using the linearization of cells along the Hilbert SFC connecting point \(\mathcal{A}\) and \(\mathcal{B}\). The list of workloads \(\mathbf{w}\) comprises the partition-cell workloads \(w_k\). Solving the CCP problem, for which \(\overline{W}=9\) is the average workload per process, the partitioning into subdomains is obtained. The domain offsets \(o_j\) are given by the splitting positions, which correspond to the first partition cell of each domain. With \(W_i\) the workload of the \(i^\text{th}\) domain, the efficiency of the partitioning is given by the maximum domain workload. Accordingly, the partition quality (Miguet1997) is assessed by
\begin{align} P &= \frac{\overline{W}}{\max_i W_i}, \label{eq:partition_quality} \end{align}
which is \(P = \frac{9}{11} \approx 82\%\) in the given example. Each partition, i.e., a continuous range of partition cells with the corresponding subtrees of the grid, is alloted to a dedicated parallel process. To prevent coarse-grained partitionings, the partition level can locally be shifted to a higher refinement level if the partition cell workload becomes too large (cf. Partition level shift). Intra-process spatial compactness of cells is implicitly ensured up to a certain degree by the locality property of the Hilbert SFC.
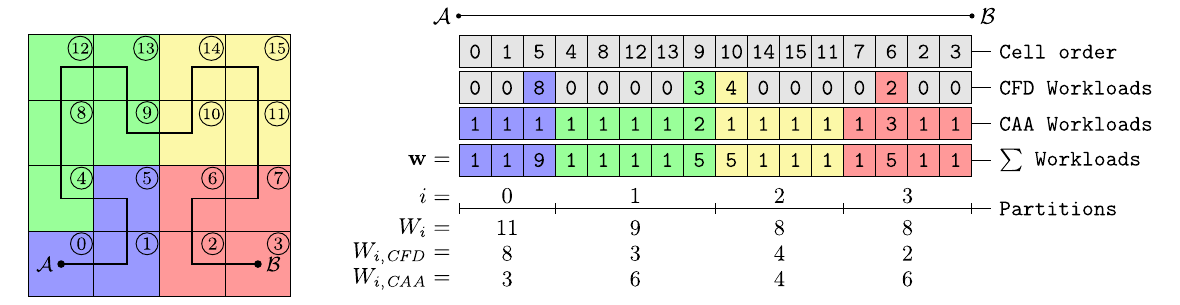
DLB partitioning approach
In general, computing a domain decomposition based on SFCs reduces to solving the resulting CCP problem. A straightforward extension for dynamic load balancing is given by estimating the computational weights for different load types during the simulation to determine new workloads as an input to the 1D partitioning problem. However, since local workload variations are not captured, the partitioning might be suboptimal in terms of performance, since any chosen CCP algorithm aims at an optimal partition quality (see Eq.~eq:partition_quality}).
However, this approach is useful for simulations in which dynamic imbalances occur, e.g., due to the use of adaptive mesh refinement. Since the mesh is constantly changing this one-shot DLB method is suitable to decently balance the time-dependent compute load, while keeping the DLB overhead reasonalbly low. That is, the cost of frequent redistributions needs to be balanced against the potential performance gains.
In the case of static imbalances, a different approach can be utilized to determine domain offsets for the SFC-based partitioning to alleviate load imbalances more rigorously.
First, the initial partitioning is improved by using the aforementioned method to obtain a reasonably good starting point for the succeeding steps. In the following repartitioning steps, the individual domain offsets are iteratively refined based on the measured load imbalance and the computed computational weights. The number of iterations for the DLB strategy to converge is highly problem dependent. Thus, for problems exhibiting a static imbalance it is rational to limit the number of iterations such that after an initial balancing phase the computation can continue with the best partitioning determined by then. As a starting point of the DLB approach, the cumulative load imbalances given by
\begin{align}\label{eq:cumulative_imbalance} s_j = \sum_{i=0}^{j-1} l_i - 1.0 \quad \forall j \in \{1,\dotsc,N\}, \quad \text{with} \quad s_0 = 0, \end{align}
are determined. Each value quantifies for the corresponding domain offset \(o_j\) the overall load imbalance of domains left and right of the splitting position. Thus, an optimal local position requires shifting the offset \(o_j\) along the SFC to minimize the cumulative imbalance. The general assumption of this approach is that by optimizing each offset individually global load balance can be obtained.
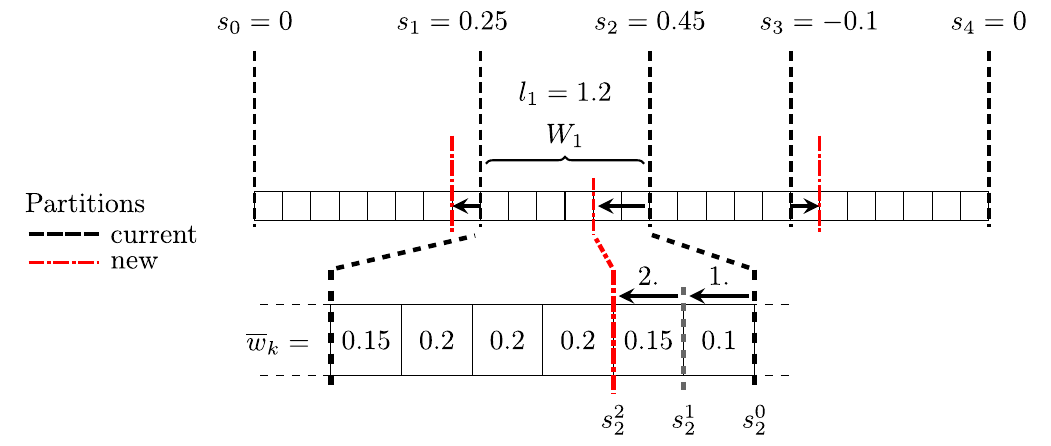
The approach is depicted in the figure above, with a list of partition cells split into four partitions. With the computational load \(l_i\) of each parallel subdomain, the cumulative imbalances \(s_j\) are computed according to Eq. \(~\ref{eq:cumulative_imbalance}\). Thus, the load discrepancy between all processes on the left and right of each splitting position is quantified. This implies, considering the value of \(s_2=0.45\) in the example, that the compute load of the first two processes is significantly higher than that of the two remaining ones. That is, the accumulated workload of process 0 and 1 is \(45\%\) above average. Therefore, by shifting the offset to the left, workload is moved from overloaded to underloaded processes. Accordingly, global load imbalances can be reduced by individually shifting each domain offset in the direction given by
\begin{align} d_j = -\text{sign} \left( s_j \right). \end{align}
The load share \(\widetilde{w}_k\) of the partition cell \(k\) on domain \(i\) is computed as
\begin{align} \widetilde{w}_k = l_i \cdot \overline{w}_k, \quad \text{with} \quad \overline{w}_k = \frac{w_k}{W_i}, \end{align}
which can be interpreted as an allocation of the load \(l_i\) onto the local partition cells. By counterbalancing the cumulative imbalance \(s_j\) with the traversed partition cell load shares
\begin{equation} \begin{split} \quad s_j^k = s_j^{k-1} + d_j \cdot f_{penalty} \cdot \widetilde{w}_{m\left(k\right)} \quad \text{for} \quad k \ge 1, \\ \text{with} \quad m\left(k\right) = o_j + d_j k - \frac{1}{2}\left(d_j+1\right) \quad \text{and} \quad s_j^0 = s_j, \end{split}\label{eq:dlb:iteration} \end{equation}
the necessary displacement of each offset \(o_j\) can be assessed by the sequence index \(k\) for which \(s_j^k \approx 0\) holds. That is, the cumulative load deviation \(s_j^0\) is balanced by the accumulated load shares \(\widetilde{w}_{m\left(k\right)}\), which are used to assess the amount of transferred workload, with \(m(k)\) the partition cell index to the sequence index \(k\). The additional penalization factor \(f_{penalty} \ge 1\) allows to limit the displacements and prevent overshooting. Thus, the DLB algorithm refines the partitioning during the simulation. This approach is illustrated in the figure and Eq. \(~\ref{eq:dlb:shift_example}\) for the second domain offset \(o_2\), using a penalty factor of \(f_{penalty} = 1.25\). According to Eq. \(~\ref{eq:dlb:iteration}\), the initial cumulative imbalance of \(s_2 = 0.45\) is minimized by shifting the offset by two partition cells, which yields the new domain offset
\begin{align} \begin{split} s_2^0 := 0.45 & \quad\Rightarrow\quad s_2^1 := 0.45 - 1.25 \cdot 1.2 \cdot 0.1 = 0.3 \\ & \quad\Rightarrow\quad s_2^2 := 0.3 - 1.25 \cdot 1.2 \cdot 0.15 = 0.075. \end{split}\label{eq:dlb:shift_example} \end{align}
When proceeding with the computation, the overload on process 0 and 1 will be reduced, since the workload of the two partition cells is transferred to the previously underloaded processes.
References
- A. Niemoeller, M. Schlottke-Lakemper, M. Meinke, W. Schroeder, Dynamic load balancing for direct-coupled multiphysics simulations, Computers and Fluids, Volume 199, 2020, 10.1016/j.compfluid.2020.104437.