Tutorial 7 (DG Solver)

Table of Contents

• Theory
• Tutorial Part I: Monopole in a boundary layer
  • Setup
  • Run
• Tutorial Part II: Co-rotating vortex pair
  • Setup
  • Run

In this part, we will run simulations with the Discontinuous Galerkin (DG) solver. The DG solver uses the Discontinuous Galerkin Methods to solve the Acoustic Perturbation Equations (APE) and predict the acoustic field of the investigated configurations. We will first run a simulation with only DG solver and then conduct a coupled simulation between the FV and DG solver.

Theory

See Theory & Implementation Discontinuous Galerkin Method (DG) old.

For more details of the equations and test case setups, please refer to our Ph.D. thesis:

• Michael Alexander Schlottke-Lakemper, 2017, A Direct-Hybrid Method for Aeroacoustic Analysis

Tutorial Part I: Monopole in a boundary layer

Setup

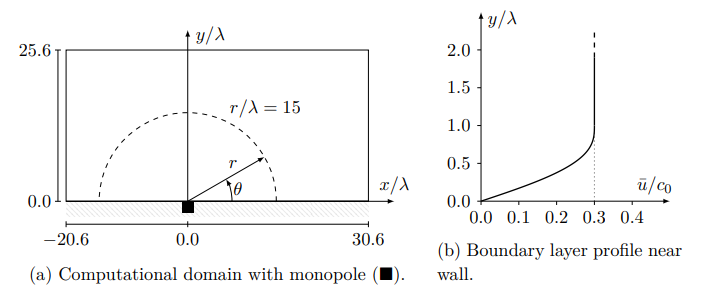
In part one, we will run a simulation with only the DG solver. For this purpose, we use the test case that has a monopole sound source in a boundary layer.

Setup for the simulation of an acoustic monopole at a plane wall, Schlottke 2017

Download the case with the command:

svn co http://svn.aia.rwth-aachen.de/maia/testcases/DG/2D_monopole_in_boundary_layer

link your MAIA binary (git version, compiled with gnu compiler in at least production mode ./configure 1 2).

Run

Generate the grid with:

./maia properties_grid.toml

Open properties_run.toml and you can see:

initialCondition = 2               # describs the boundary layer profile near the wall
ductPosition     = [-0.05, 0.05]   # describs the location and function of the acoustic monopole

Initialize the simulation with:

mpirun -np 12 ./maia properties_run.toml

After the initialization, a solution_00000010.Netcdf will be generated in the /out folder.

Next restart the simulation and run until \(tc_0/\lambda = 24 \):

mpirun -np 12 ./maia properties_restart.toml

To prevent long waiting time, a restart fiile at global timestep = 2308 is provided in the /restart folder. And the simulation runs from timestep 2308 to 2312.

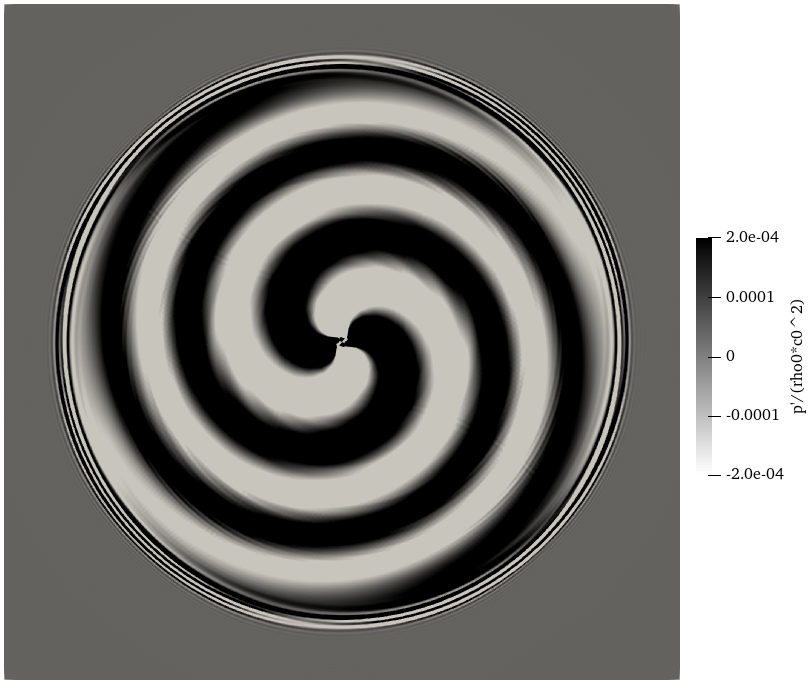
Finally open the solution_00002312.Netcdf in ParaView. Select p in the property box which represents the pressure purturbation \(p'/(\rho_0c_0^2)\) in the APE. The result should be like this:

Pressure contours, Schlottke 2017

Tutorial Part II: Co-rotating vortex pair

Setup

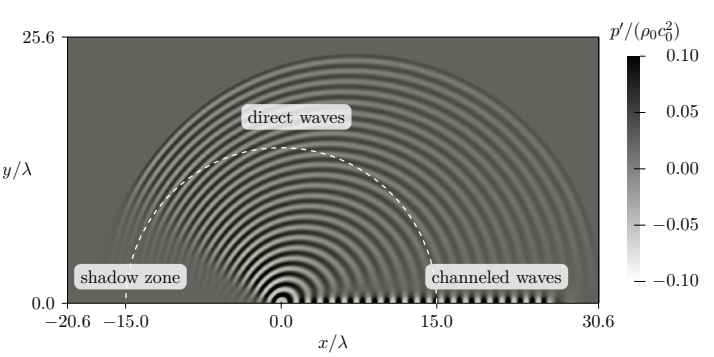
In the second part, the DG solver is coupled with the FV solver to predict the sound generated by a pair of co-rotating vortices in a quiesent meduim.

Flow setup for two co-rotating vorties, Schlottke 2017

Download the case and link you MAIA executeble in the test case folder.

svn co http://svn.aia.rwth-aachen.de/maia/testcases/DG/2D_spinning_vortex_online_coupling_nonlinear_source

Run

1.Generate mean flow field with the FV solver

• Create a new folder to save the mean file: mkdir out/fv_mean
  
• In properties_grid.fv.toml, change outputDir = "out/fv_mean/"
• Notice this property file generate two similar grid, one for the FV solver, the other for the PostData solver to compute and save mean file.

  noSolvers       = 2
  multiSolverGrid = true

• Generate the grid by ./maia properties_grid.fv.toml
• In properties_run.toml do the following changes:

  timeSteps      = 10000  # OF TIMESTEPS
   
  outputDir      = "./out/fv_mean/"   # ROOT DIR OF OUTPUT FILES
  solutionOutput = "./out/fv_mean/"   # ROOT DIR FOR SOLUTION OUTPUT
  #restartDir    = "./restart/fv/"    # Restart directory
   
  pp_averageRestartInterval = 1000    # Restart interval for averaging
   
  restartFile     = false
  restartInterval = 1000

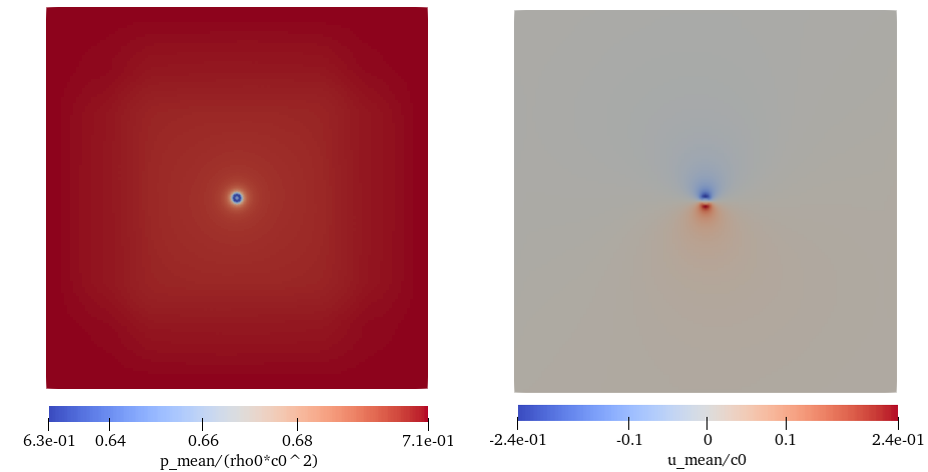
• Run the FV simulation and generate the mean file mpirun -np 12 ./maia properties_run.toml
• Open out/fv_mean/Mean_s1_00002900-00009450.Netcdf in ParaView, you can see the generated time averaged flow field.

Mean flow field

2.Run the coupled FV + DG simulation

• Generate the grid by ./maia properties_grid.toml
• In properties_restart_0.tmol, change the following properties:

  meanDataFileName = "out/fv_mean/Mean_s1_00002900-00009450.Netcdf"
  timeSteps        = 12500

• Notice sourceTerms = "q_mI" indicates that the coupled simulation reads in the mean file and calculates the perturbed Lamb vector \( L' \) as the source terms in the acoustic perperbation equaions (APE), where: \( q_m = -L'= -(w \times u)'\)
• Run the coupled simulation mpirun -np 12 ./maia properties_restart_0.toml, this could take a few minutes.
• The solution files of the DG solver is saved in out/dg/, open solution_b1_00012500.Netcdf in ParaView:
• Adjust the display range of the pressure fluctuation, you can get the following results:

Pressure contours of the co-rotating vorties