The unsteady, three-dimensional enthalpy equation for incompressible fluid in arbitrary Lagrangian-Eulerian formulation is as follows
\begin{equation} \frac{d}{dt} \int_{V} \rho H \, dV + \oint_{\partial V} (\rho H u - \lambda \nabla T) \cdot n \, d \Gamma = 0, \end{equation}
where \(H\) is the specific enthalpy and \(\lambda\) the thermal conductivity.
In this convection-diffusion equation, the diffusive part, also known as Fourier's law of heat conduction, is a parabolic partial differential equation and the convective part is a hyperbolic partial differential equation. The numerical solution is determined by which of the two parts is dominant.
The system of equations is completed by specific material databases in order to establish the following relations \(H = f(T)\) and \(\lambda = f(T)\), this eliminates the need to explicitly resolve the phase boundary. The enthalpy temperature linkage already implicitly includes the latent heat release due to the phase transition and structural changes, which cannot be described analytically for the various mixtures respectively alloys in general. The following graph shows the temperature to enthalpy curve for three different steel grades.
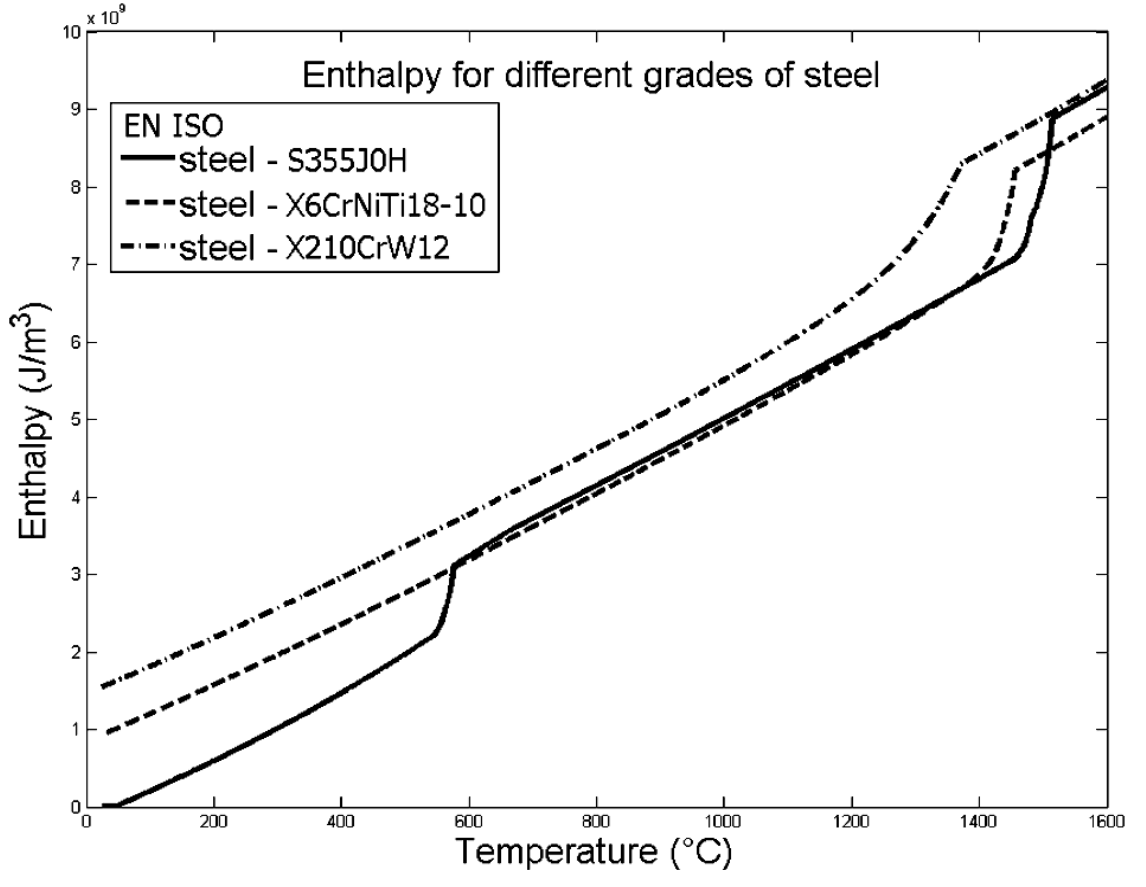
In the presented version the density \(\rho\) is assumed to be constant and also the convection velocity \(u\) is uniform over the computational domain.
References
- Mauder, Tomas & Sandera, Cenek & Stetina, Josef & Milos, Seda. (2011). Optimization of the quality of continuously cast steel slabs using the firefly algorithm. Materiali in Tehnologije. 45. 347-350. https://www.researchgate.net/publication/235643301_Optimization_of_the_quality_of_continuously_cast_steel_slabs_using_the_firefly_algorithm